二酸化炭素分子の一次元振動
シミュレーション
赤丸が酸素原子、緑丸が炭素原子
白線と黄色線は原子間を結ぶ「バネ」(見やすさのために色を変えている)
初期状態は $C_1 = 1, C_2 = 0.2$
シミュレートしているもの
このシミュレーションでは、二酸化炭素分子の古典的な一次元振動をシミュレートしている。簡単に言えば、次のような問題を考えている:
質量 $12m, 16m, 12m$ の3質点が、ばね定数 $k$ の2本のばねで直線状につながれている。 このような系の一次元方運動はどのようになっているか?
結論として、上のシミュレーションでは、以下の一般解に基づいて描画を行っている:
\[\begin{align} \left\{ \begin{array}{l} x_1(t) = C_1\cos(\omega_1 t) + C_2\cos(\omega_2 t) \\ x_2(t) = -\frac{8}{3}C_2\cos(\omega_2 t) \\ x_3(t) = - C_1\cos(\omega_1 t) + C_2\cos(\omega_2 t) \end{array} \right. \\ with \quad \omega_1 = \frac{1}{4}\sqrt{\frac{k}{m}}, \quad \omega_2 = \frac{1}{4}\sqrt{\frac{11}{3}\frac{k}{m}} \nonumber \end{align}\]$\omega_1, \omega_2$ は系の2つの固有振動数。$C_1, C_2$ は各固有振動の振幅(定数)で、シミュレーションでは変更することができる。
詳細は下で説明する。
シミュレーションのソースコード
JavaScript で動いています。ソースコードはこちら。
説明
以下の道筋で運動の一般解を導く:
- 運動方程式を立てる
- 運動方程式を整理する
- 基準振動を求める
- 基準振動の重ね合わせが一般解
※すべての事柄は説明しきれません。そのため、振動や関する基礎知識があり行列の簡単な計算ができる、という前提での説明となっております。
運動方程式の導出
まず、運動方程式を導く。2通りの方法でやってみる:
- 高校物理だけを使う
- ラグランジアンを使う
高校物理で運動方程式を導出
各質点の受ける力(弾性力)を考えれば、運動方程式を立てられる:
\[\begin{align} \begin{cases} 16m\ddot{x_1} &= k(x_2 - x_1) = -kx_1 + kx_2 \\ 12m\ddot{x_2} &= k(x_3 - x_2) - k(x_2 - x_1) = kx_1 - 2kx_2 + kx_3 \\ 16m\ddot{x_3} &= - k(x_3 - x_2) = kx_2 - kx_3 \end{cases} \end{align}\]ラグランジアンから運動方程式を導出
ラグランジアン $L$ は
\[\begin{align} &L \nonumber \\ =& \frac{1}{2}\cdot 16m\cdot\dot{x_1}^2 + \frac{1}{2}\cdot 12m\cdot\dot{x_2}^2 + \frac{1}{2}\cdot 16m\cdot\dot{x_3}^2 -\frac{1}{2}k(x_2-x_1)^2 - \frac{1}{2}k(x_3-x_2)^2 \nonumber \\ =& m(8\dot{x_1}^2 + 6\dot{x_2}^2 + 8\dot{x_3}^2) - \frac{1}{2}k(x_1^2+2x_2^2+x_3^2-2x_1x_2-2x_2x_3) \end{align}\]よって、各質点に対する運動方程式は
\[\begin{align} \begin{cases} \dv{}{t}\left(\pdv{L}{\dot{x_1}}\right) - \pdv{L}{x_1} &= 16m\ddot{x_1} + kx_1- kx_2 = 0 \\ \dv{}{t}\left(\pdv{L}{\dot{x_2}}\right) - \pdv{L}{x_2} &= 12m\ddot{x_2} +2kx_2 - kx_1 - kx_3 = 0 \\ \dv{}{t}\left(\pdv{L}{\dot{x_3}}\right) - \pdv{L}{x_3} &= 16m\ddot{x_3} + kx_3- kx_2 = 0 \end{cases} \end{align}\]運動方程式の整理
運動方程式が導かれたので、これを解けば良い。しかし、$x_1, x_2, x_3$ の3変数が混在するまま解くのは面倒。そこで、重心の情報を使うことで式を簡単にしてから解くことにする。
重心の情報
系の重心は、外力を受けない限り等速直線運動または静止する。そこで、系の重心は静止してて、その座標は一定であるとする。更にその値は任意にとって構わないから、重心座標は $0$ であるとする:
\[\begin{align} \frac{16mx_1 + 12mx_2 + 16x_3}{16m+12m+16m} = 0 \end{align}\]この式より、次の関係が得られる:
\[\begin{align} x_2 = - \frac{4}{3}\left(x_1 + x_3\right) \end{align}\]式の整理
直前で得られた関係式を運動方程式に代入する。すると、独立な方程式として次の2本が得られる:
\[\begin{align} \begin{cases} 16m\ddot{x_1} + kx_1 + \frac{4}{3}k\left(x_1 + x_3\right) = 16m\ddot{x_1} + \frac{7}{3}kx_1 + \frac{4}{3}kx_3 = 0 \\ 16m\ddot{x_3} + kx_3 + \frac{4}{3}k\left(x_1 + x_3\right) = 16m\ddot{x_3} + \frac{4}{3}kx_1 + \frac{7}{3}kx_3 = 0 \end{cases} \end{align}\]$x_2$ についての運動方程式を変形したものは $x_1, x_3$ についての式の和になっている(=独立な式ではない)ことに注意。
基準振動
新たに求まった連立方程式を使って、基準振動(モード)を求める。系の基準振動とは、系の運動が単振動のみで表される状態のこと。系の基準振動の振動数を $\omega$ とおき、$C, \phi$ を定数とすれば、$x_1, x_3$ に関する基準振動の運動は以下で記述される:
\[\begin{align} \begin{cases} x_1 = C\cos\left(\omega t + \phi\right)\\ x_3 = C\cos\left(\omega t + \phi\right) \end{cases} \end{align}\]$C$ は振幅であり、$\phi$ は位相に対応する。これらを、式 $(7)$ に代入し、整理する:
\[\begin{align} \begin{cases} \left(-16m\omega^2 + \dfrac{7}{3}k\right)A_1 + \dfrac{4}{3}kA_3 = 0 \\\\ \dfrac{4}{3}kA_1 + \left(-16m\omega^2 + \dfrac{7}{3}k\right)A_3 = 0 \end{cases} \end{align}\]整理の際は、$\ddot{x_1} = -\omega^2 A_1\cos\left(\omega t + \phi\right) = -\omega^2 x_1$ などと計算すれば微分が消える。
$(A_1, A_2) = (0, 0)$ では全質点が静止する解しか求まらないから、そうではない $\omega$ を求める。ここでは、連立方程式を行列に直して解くことにする。
\[\begin{align} \begin{bmatrix} -16m\omega^2 + \dfrac{7}{3}k & \dfrac{4}{3}k \\ \dfrac{4}{3}k & -16m\omega^2 + \dfrac{7}{3}k \end{bmatrix} \begin{bmatrix} A_1 \\ A_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{align}\]行列が逆行列を持たなければ、$(A_1, A_2) \neq (0, 0)$ 以外の解が出てくので、次のように計算できる:
\[\begin{gather} \det \begin{bmatrix} -16m\omega^2 + \dfrac{7}{3}k & \dfrac{4}{3}k \\ \dfrac{4}{3}k & -16m\omega^2 + \dfrac{7}{3}k \end{bmatrix} = 0 \\\nonumber\\ \therefore~ \left(-16m\omega^2 + \frac{7}{3}k\right)\left(-16m\omega^2 + \frac{7}{3}k\right) - \frac{4}{3}k\cdot\frac{4}{3}k = 0 \\\nonumber\\ \therefore~ \boxed{\omega = \frac{1}{4}\sqrt{\frac{k}{m}}, \frac{1}{4}\sqrt{\frac{11}{3}\frac{k}{m}}} \end{gather}\]求まった $\omega$ を式 $(8)$ に代入すれば、$x_1, x_3$ の基準振動が得られるし、式 $(6)$ を利用すれば $x_2$ の基準振動も得られる。
基準振動1
一つ目の基準振動($\omega = \omega_1 = \frac{1}{4}\sqrt{\frac{k}{m}}$)は、$C_1, \phi_1$ を定数として次の通りに表される:
\[\begin{align} \begin{cases} x_1 = C_1\cos(\omega_1 t + \phi_1) \\ x_2 = 0 \\ x_3 = -C_1\cos(\omega_1 t + \phi_1) \end{cases} \end{align}\]これは、下のような振動。
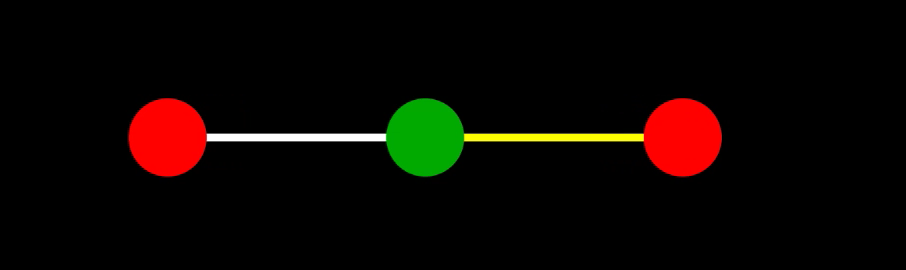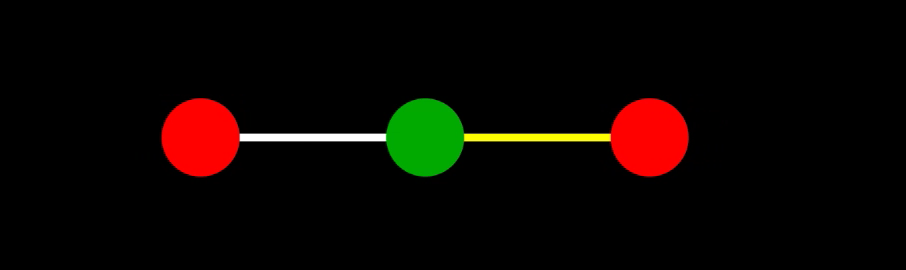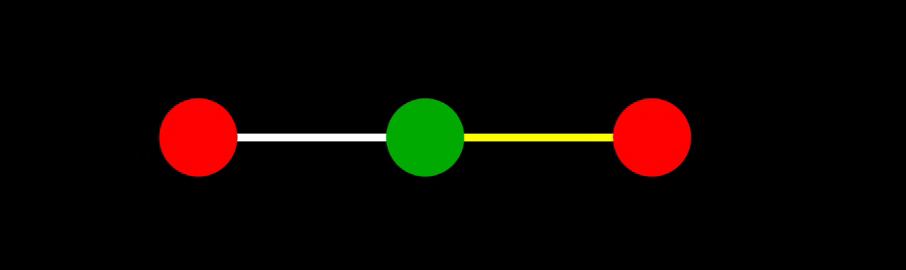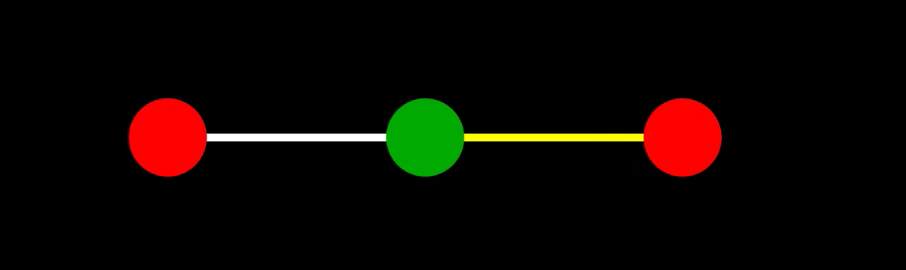
基準振動2
二つ目の基準振動($\omega = \omega_2 = \frac{1}{4}\sqrt{\frac{11}{3}\frac{k}{m}}$)は、$C_2, \phi_2$ を定数として次の通りに表される:
\[\begin{align} \begin{cases} x_1 = C_2\cos(\omega_2 t + \phi_2) \\ x_2 = -\frac{8}{3}C_2\cos(\omega_2 t + \phi_2) \\ x_3 = C_2\cos(\omega_2 t + \phi_2) \end{cases} \end{align}\]これは、下のような振動。
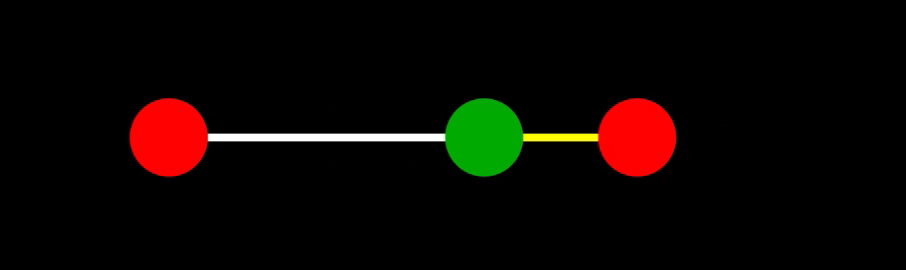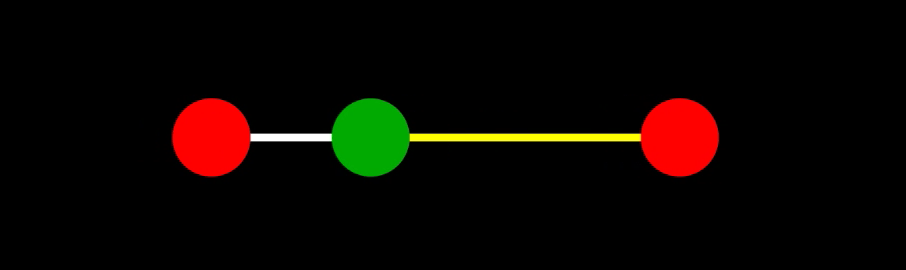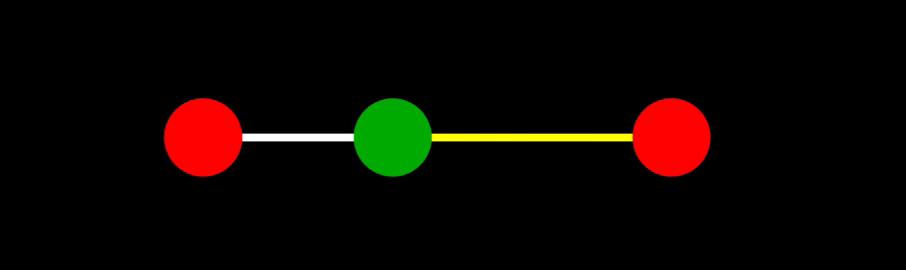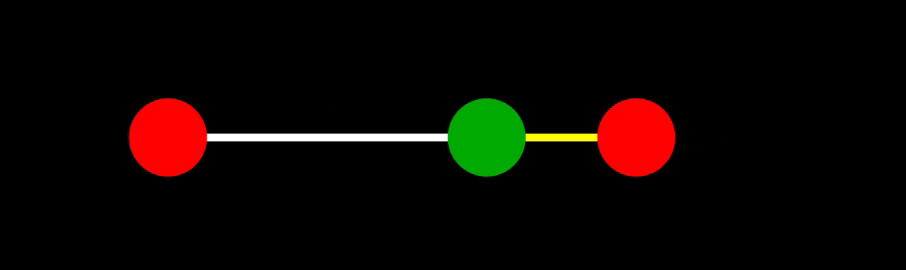
運動の一般解
運動の一般解は、基準振動の重ね合わせである。よって、$\omega_1, \omega_2$ を系の固有振動数、$C_1, C_2$ を振幅(定数)、$\phi_1, \phi_2$ を位相(定数)として、運動の一般解は次のようになる:
\[\begin{align} \left\{ \begin{array}{l} x_1(t) = C_1\cos(\omega_1 t + \phi_1) + C_2\cos(\omega_2 t + \phi_2) \\ x_2(t) = -\frac{8}{3}C_2\cos(\omega_2 t + \phi_2) \\ x_3(t) = - C_1\cos(\omega_1 t + \phi_1) + C_2\cos(\omega_2 t + \phi_2) \end{array} \right. \\ with \quad \omega_1 = \frac{1}{4}\sqrt{\frac{k}{m}}, \quad \omega_2 = \frac{1}{4}\sqrt{\frac{11}{3}\frac{k}{m}} \nonumber \end{align}\]本シミュレーションの場合
本シミュレーションでは、$\phi_1 = \phi_2 = 0$ としている。すなわち、次の運動をシミュレートしている:
\[\begin{align} \left\{ \begin{array}{l} x_1(t) = C_1\cos(\omega_1 t) + C_2\cos(\omega_2 t) \\ x_2(t) = -\frac{8}{3}C_2\cos(\omega_2 t) \\ x_3(t) = - C_1\cos(\omega_1 t) + C_2\cos(\omega_2 t) \end{array} \right. \end{align}\]シミュレーション結果はページ冒頭に掲げた通り。